花粉症はなぜ起こるの？

異物から体を守る仕組み

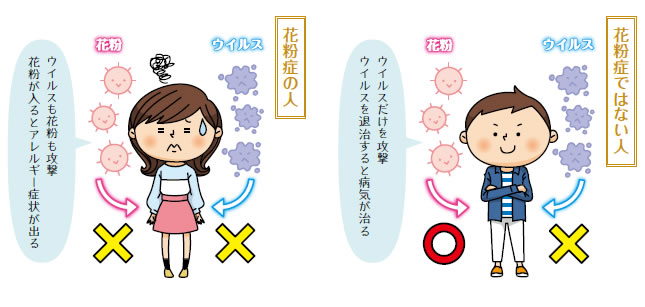
　風邪をひくと、熱が出たり、咳や鼻水が止まらなくなったりしますよね。これは、有害なウイルスや細菌から体を守るための仕組みによるものです。体にとって有害な異物が侵入してくと、熱によって退治しようとしたり、咳や鼻水によって体外に追い出そうとしたりして、それらを攻撃するのです。一度侵入してきたものに対しては、抗体という武器が作られ、次からは侵入を未然に防いだり簡単に排除したりできるようになって、病気にかかりにくくなったり治りやすくなったりします。これを免疫といいます。
　花粉症も同じ仕組みによって起こります。本来なら、花粉は異物ではあるものの有害ではないため、体に入ってきても攻撃はしません。しかし、入ってくる花粉の量が多くなると体が混乱して有害なものだと勘違いし、抗体を作って攻撃するようになってしまいます。抗体を作っても、有害な異物とは違い、侵入を防いだり排除したりできるようにはならないので、対象となった異物が入ってくる度に攻撃を繰り返し、繰り返しているうちに攻撃はどんどん激しくなっていきます。このように、本来は有害ではないはずのものを攻撃してしまうのがアレルギーで、花粉症はアレルギーのひとつです。

なりやすい人・なりにくい人

　花粉症の発症には個人差があります。これは、体が有害だと判断するまでの花粉の量が人によって違うからです。花粉症は、グラスに水がたまるようなものだと言われます。最初のうちは急に多くの水が入っても溢れませんが、グラスの縁まで水が満ちたら次に入るのがどんなに少ない量でも溢れてしまいます。花粉も同じで、その人の持っている容器に限界がくると溢れてしまいます。入ってくる花粉が多い環境だったり、持っている容器が小さかったりすると、すぐに溢れてしまうというわけです。
　容器が小さい、つまり花粉症になりやすい人については、元々アレルギー体質だったり、両親が花粉症だったりすると可能性が高いと言われています。また、食生活が乱れていたり、睡眠不足だったり、生活リズムが崩れている人も花粉症になりやすいことがわかっています。他に、生活環境が清潔になって有害な細菌が減った結果、有害な異物に対して抗体を作るバランスと、有害でない異物に対して抗体を作るバランスが狂ってしまう人が増えたという説などもあります。
　ですが、これらに当てはまらなかったとしても、花粉症になる可能性はあります。たとえ花粉の少ない環境で大きな容器を持っていたとしても、絶対に溢れることがないとは言い切れません。個人差があるものだからこそ、いつ溢れてしまうかは誰にもわからないのです。今、花粉症ではないからといって油断をせずに、予防や対策の知識を持っておきましょう。

原因となる植物や時期は様々

　日本で一番多いのはスギによるものですが、花粉症の原因となる植物はスギだけではありません。他にも多くの原因植物が発見されており、症状が出る時期もそれぞれ違います。代表的なものは、スギ、ヒノキ、ブタクサ、イネ科の植物などで、スギ花粉のシーズンの１～４月が終わると、ヒノキの花粉が飛び、それが過ぎるとイネ科の植物、秋になるとブタクサの花粉が飛び始めます。このように、原因となる花粉はほぼ一年中飛んでいるのです。
　花粉症の発症に個人差があるのと同じように、原因となる植物にも個人差があります。花粉症は春先だけのものだと思い込まず、目がかゆい、鼻水が止まらない、外に出た時に症状がひどくなるなど、花粉症かもしれないと感じることがあれば、病院で検査を受けましょう。充分な対策をするには、まず自分の症状の原因を知ることが必要です。

食物アレルギーを引き起こす可能性も

　一度何かでアレルギーが起こると、他のものでもアレルギーを起こしやすくなることが知られています。花粉症の場合、スギならトマト、ブタクサならメロンなど、似た性質を持つ食物に対してもアレルギー反応が出てしまうことがあるのです。
　花粉症で命に関わることはありませんが、食物アレルギーは、突然全身に反応が起こって呼吸困難になるなど、症状が急激に悪化するアナフィラキシーショックという重大な状態に陥ってしまう危険性があります。食事の時、喉のかゆみなどの違和感がないか注意しましょう。

花粉症にはどのような対策があるの？

セルフケアとメディカルケア

　花粉症の対策には、マスクの着用など自分でできるセルフケアと、薬の処方など病院で治療を受けるメディカルケアがあります。片方だけではなく、両方を取り入れる必要がありますが、全てを完璧にやろうとして続かないのでは意味がありません。自分の症状に合わせ、無理のない範囲で行うことが大事です。
　そのためにも、まずは自分の症状をきちんと把握しておくこと。一番つらい症状は何か、どんな時に症状がひどくなるのかなどをあらかじめ確認し、治療を受ける時に相談しやすいようメモをとっておくといいでしょう。

花粉を入れないようにしよう

　セルフケアの基本は、花粉を体に入れないことです。外出した時だけではなく、家の中にいる時でも花粉を吸い込まないよう注意する必要があります。
　具体的には、次のようなことに気を付けましょう。

①屋外での対策

　　花粉は、目、鼻、口から入ってくるので、外出する時はマスクやメガネを着けてこれらを覆いましょう。目が細かいマスクや、ゴーグル状になっているメガネなど、花粉症用のものを選ぶとより効果的です。また、髪や服に花粉がつくと後から吸い込んでしまうことがあります。髪はまとめて帽子をかぶる、ツルツルとした素材の服を着るなど、花粉がつきにくい服装を心がけ、家に入る前に髪や服についた花粉を払い落とします。それから、うがい、手洗い、洗顔をして花粉を洗い流しましょう。

②室内での対策

　家の中では、花粉を持ち込まないように注意します。洗濯物は花粉がつくのを避けるため、室内に干しましょう。布団を外に干した場合は、掃除機などで花粉を取り除いてから取り込みましょう。花粉がたまりやすい部屋の隅や絨毯などもこまめに掃除するといいですが、ただ掃除機をかけるだけでは、排気によって空気中に舞い上がった花粉を吸い込みやすくなってしまうことがあります。雑巾などで水拭きもしましょう。また、空気清浄機や加湿器の設置もおすすめです。空気清浄機は空気中の花粉を取り除け、加湿によって水分を含んだ花粉は床に落ちて舞い上がらなくなります。

生活習慣を見直そう

　花粉を入れないことの他に、体調を整えておくことも大切です。花粉症などのアレルギーは、体調が悪いと症状がひどくなる傾向があります。風邪をひくことなどがないよう、偏った食事や睡眠不足を避け、生活リズムを整えましょう。

治療は早めに取りかかろう

　今の花粉症の治療は、花粉が飛び始める前に治療を始める初期療法が主流です。花粉症は、繰り返し花粉を吸い込むうちに症状がひどくなり、症状がひどくなってしまってからでは薬が効きにくくなってしまいます。また、いつ症状が出るか予測できない風邪などとは違い、症状が出始める時期が予測できます。そのため、花粉が飛び始める前や、症状の軽いうちに薬を飲むという治療法が有効なのです。早い段階で薬を飲んでおくと、症状が出なかったり、出ても軽くすんだりします。
　花粉が飛び始める時期や花粉の量は、地域や年によって違いがありますが、スギ花粉が飛び始めるのは概ね１月下旬から２月初め頃で、この頃に治療を始めるのがいいとされています。スギ花粉の飛散時期が近づくと、ニュースや天気予報でも情報が発信されるようになります。これらをチェックして、花粉症かもしれないと感じたら、すぐに病院に行きましょう。
　また、たとえ早めに治療が始められなくても、諦めることはありません。花粉症は一度発症すると毎年起こるものなので、今年間に合わなければ、来年、早い時期に病院に行けばいいのです。

自分に合った治療を選ぼう

　花粉症の症状は個人差が大きいので、目のかゆみが強ければ眼科、鼻水や鼻づまりがひどければ耳鼻科というように、自分の症状に合った病院で治療を受けましょう。治療法も、先に述べた初期療法などで症状を抑えて花粉のシーズンだけを乗り切るものと、花粉症自体を治す免疫療法があります。免疫療法とは、花粉の成分を薄めた薬を普通は花粉が入ってこない舌下や皮膚などから入れ、だんだん慣れさせていくというものです。花粉症を治す唯一の方法ですが、治療に何年もかかったり、症状が出始めると治療が始められなかったりします。また、現在は一般の薬局で買える花粉症の薬も増えています。市販の薬で充分に症状が抑えられていて、自分に合っていると思えば、それも選択肢のひとつです。
　いずれにせよ、自分の体質や症状がどのようなものかきちんと理解し、自分に合った対策をとることが最も重要です。スギ花粉による花粉症のピークは２月から４月にかけてなので、受験シーズンとも重なります。試験当日に症状が強く出て集中できなかったり、薬の副作用で眠くなってしまったりといった事態を避け、万全の態勢で臨めるように対策を考えておきましょう。

自分で自分を守れるようになってほしい

　古谷先生は、花粉症をはじめとするアレルギーについて、子どもたち自身が理解して対応していくことが必要だと考えています。実際に小中学生を対象として花粉・アレルギー策の授業をされた際のお話を伺いました。

子どもたちの命を守るために

──アレルギー対策の授業を行おうと思われたきっかけを教えてください。

　２０１２年、学校給食での食物アレルギーによる児童の死亡事故が起こりました。現場の教員として予期していなかったできごとで大変な衝撃を受けました。事故の後、各方面で学校給食における食物アレルギーへの対応が示されましたが、ほとんどが学校職員や給食調理者、保護者などの大人の対応についてでした。私は、大人だけではなく、本人を含めた子ども、周りの友達も気を付けてあげられるようにすることで事故も防げるのではないかと思いました。それからずっと、同じような事故がこの先二度と起こらないよう、子どもたちにアレルギーについて教えられるような授業ができればと思っていました。
　また、私自身もそばアレルギーを持っているのですが、中学生の頃にそばを食べて発疹が出てアレルギーだと気付いたにもかかわらず、高校生になって大きくなったからもう大丈夫だろうと食べてしまい、呼吸困難に陥るほどの症状が出たことがあります。回数を重ねるほどひどくなることなど、自身のアレルギーについての知識がなかったせいで起こったできごとでした。だからこそ、アレルギー対策には本人の理解と対処が必要だと実感しています。
　そう考えてはいても、実際に授業を行う機会にはなかなか恵まれませんでしたが、花粉症対策メガネも作っているメガネ・アイウェアブランドの株式会社ジンズの協力を得て実現することができました。

他人ごとではなく自分ごととして

──授業をするにあたって工夫した点などはありますか？

　問いを立てて、それを解決していくという形で、子どもたちが積極的に考え、順を追って学べるように意識しました。花粉症や食物アレルギーといった身近な例を取り上げ、アレルギーが起こる仕組みをアニメ動画にして用いるなど、わかりやすく親しみやすい授業になるよう心がけました。

──実際の授業はどのような様子だったかお聞かせください。

　どの子も熱心に授業に取り組んでいました。中学校では、養護教諭が実際にアレルギーのある生徒の例なども出しながら授業をしたので、身近なこととして理解しやすかったようです。また、アレルギーのある子だけではなく、アレルギーのない子も大変さをよく理解してくれました。大人になってからも食物アレルギーになる可能性があるとは思っていなかった子も多かったので、今はなっていなくても関係がないわけではないと知り、他人ごとではなく自分ごととして捉えてくれたように思います。

──今後こういった授業は増えていくのでしょうか？

　新学習指導要領に、食物アレルギーなどの基本的な理解が必要であると挙げられてはいますが、具体的な指導法は示されておらず、教材もないため、現状ほとんど行われていません。企業教育研究会では、食物アレルギーについても取り上げた「食育の時間＋」というデジタル教材の制作に携わり、授業支援を行っていますが、授業時間の確保が難しいという声が多いです。
　将来的には指導要領にも具体的な指導法が示されることが望ましいですが、今すぐというわけにはいきませんので、子どもたち自身が自分ごととして積極的に取り組んでいってくれればと思っています。

多様性のひとつとして理解を

──関塾生の皆さんへメッセージをお願いします。

　問題の解き方とは違い、体の整え方というのは先生に教えてもらえるものではありません。自分の体質や病気について理解して、どのように対応すればいいのかを知っておきましょう。受験の時にくしゃみが止まらないなど、いざ勝負しなければならない時に症状が強く出てしまったら困りますよね。薬を飲んで眠くなってしまうことだって考えられます。そうならないためにはどうすればいいのか、ちゃんと考えて、日頃から対策していくことが重要です。
　また、自分が克服していくことと同じくらい、周りが理解して接してあげることも大切です。アレルギーや病気だけではなく、コミュニケーション障害や＊ＬＧＢＴの問題など、多くの人が何らかの生きにくさを感じています。これからの社会では、自分とは違う生きにくさを抱えた人を理解して、受け入れることが大切になっていきます。それが多様性を理解することにつながります。そして、そのためには正しい知識が必要です。様々な知識を身に付けて、それぞれに合った対応ができるようになってください。

＊恋愛対象や自己の認識など、何らかの意味で「性」のあり方が多数派と異なる人のこと。

• 特集①
• わたしの勉学時代
• 特集②
• イラストレーションギャラリー