2021年5月号特集②　算数オリンピック

　世界の子どもたちに、算数をゲームやスポーツと同じように楽しんでもらいたい――算数オリンピックは、こんな願いのもと誕生しました。国境・言語・人種の壁を超え、地球上のすべての子どもたちが、算数という“万国共通”の種目で思考力と独創性を競い合う「小学生・中学生の知の祭典」、それが算数オリンピックです。１９９２年に第１回大会が行われてから毎年開催されており、第30回目となる今年は、トライアル地方大会が６月13日に、ファイナル決勝大会は７月18日に行われる予定です。
　今回は、算数オリンピックの種目や、過去問題を紹介します。気軽にトライしてくださいね！

世界的数学者・広中平祐氏が提唱
　算数オリンピックを提唱したのは、広中平祐氏（１９３１年生まれ。京都大学理学部卒業。京都大学名誉教授、ハーバード大学名誉教授）。数学界のノーベル賞と言われるフィールズ賞と、文化勲章も受賞している世界的数学者です。毎年、算数オリンピックの大会会長を務め、未来を担う新しい才能と人材を発見することを楽しみにしているそうです。

大会は現在５種目

　スタートした当初は、小学６年生を主な対象とした算数オリンピック１種目だけでしたが、現在は対象学年によって５種目に分かれています。
　それぞれ、トライアル地方大会とファイナル決勝大会の２段階に分けて実施され、トライアル地方大会を通過しなければファイナル決勝大会には進めません。ファイナル決勝大会進出者（ファイナリスト）には認定証（キッズＢＥＥファイナリストにはメダルも）が授与され、キッズＢＥＥ以外の４種目の入賞者にはメダルやトロフィーなどが贈られます。
　ゲームやスポーツに参加する感覚でチャレンジしてみませんか？

　　　　　　　　　　大会種目　　　　　　　　　　
●キッズBEE（小学１～３年生対象）
　未就学児童は参加できません。
●ジュニア算数オリンピック（小学５年生以下対象）
　小学５年生以下なら誰でも参加できます。
●算数オリンピック（小学６年生以下対象）
　小学生なら誰でも参加できます。
●ジュニア広中杯（中学１・２年生対象）
　中学１・２年生のみが参加できます。
●広中杯（中学３年生以下対象）
　中学生なら誰でも参加できます。
※出場できるのは１種目のみです。

くわしくはこちら↓
https://www.sansu-olympic.gr.jp/
一般財団法人算数オリンピック委員会

過去問題に挑戦！

【問題１】
□の中に１～11の数字を１つずつ入れて、たて、よこの計算式を完成させなさい。（４、７、８、11はすでに入っています）
〈2009年度ジュニア算数オリンピックトライアル問題〉

【問題2】
０～９が書かれたカードを１枚ずつ、よこ一列に並べました。
すると、どのとなり合う２枚のカードを見ても、その差は３か５のどちらかでした。

上のように、左端が０、右端が１のとき、残りの８個の数字を正しく並べなさい。
〈2016年度算数オリンピックトライアル問題〉

【問題3】
たて、よこ、ななめの３つのマス内の数字の和がすべて異なるように、０～８を各１個ずつ入れます。
黄色の４つのマスには奇数の数字を入れます。
いま、０、３、６が図のように入っています。
このとき、残りの１、２、４、５、７、８を入れなさい。
〈2012年度算数オリンピックファイナル問題〉

【問題4】
半径２の円を７個、図のように外接させます（どの円も２つ以上の円と外接しています）。
さらに、図のように正三角形を円と接するように描くとき、大きい方の正三角形と小さい方の正三角形の周の長さの差を求めなさい。
〈2017年度ジュニア広中杯トライアル問題〉

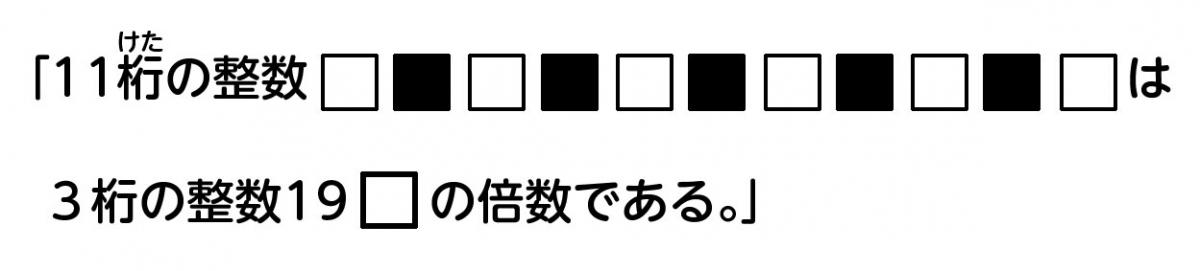
【問題5】
下の７つの □ には同じ数字が入り、５つの ■ にも同じ数字が入ります。
ただし、入る数字は、１、２、３、４、５、６、７、８、９のいずれかです。
文章が正しくなるように、空欄に数字を補いなさい。（答えは１組の例だけでよい）
〈2017年度ジュニア広中杯ファイナル問題〉

問題１の答え

解説
下図のように空欄のマスに入る数字をア～キとします。
ア～キの中で10である可能性があるものはイとオとカです。
◆イが10の場合
４－ア＋10＝11より、アは３とわかります。
アが３なので、３＋エ＝７より、エが４となります。
しかし、４はすでに入っているので、イが10ではないとわかります。
◆オが10の場合
オが10とすると、ウ＋エ＝18です。
しかし、すでに11と10と８が使われているためにウ＋エは最大でも、
９＋７＝16にしかなりません。よって、オも10ではないとわかります。
◆カが10の場合
４＋ウ＝10より、ウが６とわかります。次に、イは８より大きい数のはずです。
８より大きい数で使われていないのは、９しかないので、イは９とわかります。
すると、９－８＝キなので、キが１とわかり、４－ア＋９＝11より、
アが２とわかります。
最後に、２＋エ＝７より、エが５とわかり、６＋５－８＝オより、
オが３とわかります。

問題２の答え

解説
それぞれの数からつなげられる数を表したのが、下の図です。
ここで、２、７、８、９は両端ではないので、上の図を見ると、10枚の並び方のどこかに、「527または725」「274または472」「385または583」「496または694」の並びがすべて入ることがわかります。
これに注意すると、「38527496または69472583」の並びが入ることが決まります。
左端が０、右端が１なので、これにうまくつながるのは、「38527496」となります。

問題３の答え

解説
空欄にA～Fを入れて考えます。
黄色のマスには奇数が入るので、Ｂ、Ｄ、Ｅには、１、５、７が入ります。
ここで、すべての和が異なるので、Ｂ＋C＋Ｅと、３＋Ｃ＋Ｄも異なります。
つまり、Ｂ＋Ｅと３＋Ｄは異なります。よって、Ｄには５が入りません。
◆Ｄ＝７の場合
ＢとＥには１と５が入ります。よって、Ｂ＋Ｅ＝６となります。
すると、０＋Ｃ＋６＝Ｂ＋Ｃ＋Ｅとなってしまい、題意を満たしません。
◆Ｄ＝１の場合
ＢとＥには５と７が入ります。また、Ａ＋Ｃ＋Ｆ＝２＋４＋８＝14です。
そのため、Ｃが２の場合は、Ｂ＋Ｃ＋Ｅ＝14となり、Ｃが８の場合は、
０＋８＋６＝14となり、題意を満たしません。よって、Ｃ＝４と決まります。
次に、Ｅ＝７の場合、６＋Ｄ＝０＋Ｅなので、６＋Ｄ＋Ｆ＝０＋Ｅ＋Ｆとなってしまいます。よって、Ｅ＝５とわかります。
このことから、残りの７はＢに入ります。
残ったＡとＦを考えると、Ａ＝８、Ｆ＝２のときのみ、題意を満たします。

問題４の答え

解説
大きい方の正三角形と小さい方の正三角形には、下図のように半径２の円が接します。

図に赤い線で示した三角形は合同なので、２つの正三角形の一辺の長さの差は、線分ＢＣの長さと線分ＧＨの長さの差、すなわち、円の直径４に等しく、周の長さの差は、４×３＝12となります。

問題５の答え

□＝６　■＝７
□＝８　■＝３
□＝７　■＝８
※どれか１組を答えればよい。

解説
196＝14＾2に注目して、 □ を６とすると、
11桁の数は７の倍数である必要がありますが、
60606060606＝60606×1000001＝７×8658×1000001が
７の倍数であることと、101010101が７の倍数でないことから、
■ は７としなければなりません。
このとき、67676767676＝196×345289631より、
与えられた文章は正しいことがわかります。
よって、空欄に補う数字として、 □ ＝６、 ■ ＝７が見つかります。

※他に、 □ ＝８、 ■ ＝３と □ ＝７、 ■ ＝８があり、
　これ以外にはありません。